Useful Properties To Check With Fuzz Testing

The is part three of a three part series on Property-based fuzz testing. Part one introduces property-based testing. Part two discusses property-based fuzzing.
This article lists a number of useful properties that are commonly used to validate the correctness and safety of code. If you are not sure how to apply property-based fuzzing to your code, this list should give you some inspiration.
The function does not explode
The simplest property, and a surprisingly useful one, is simply checking that the code does not result in an unexpected exception:
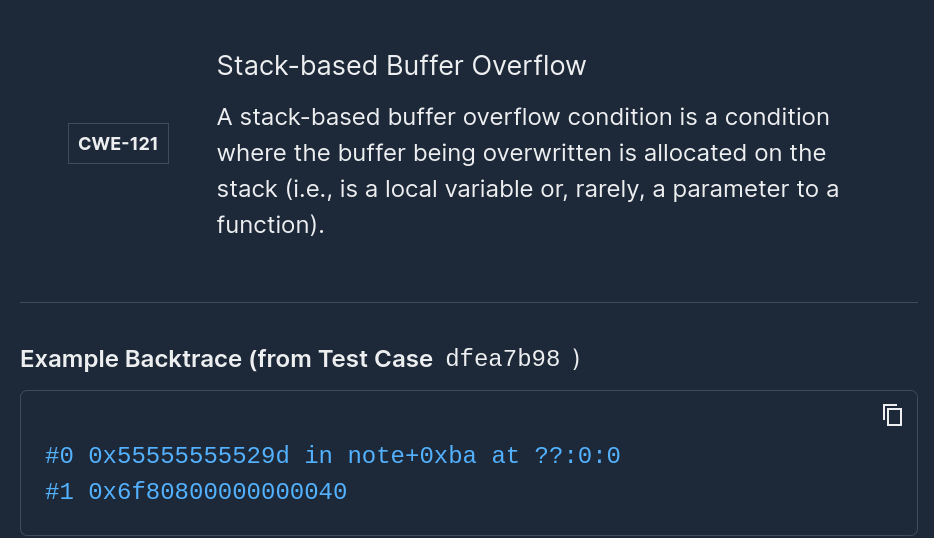
That simple property can sometimes find vulnerabilities. For instance, if there was a SQL injection in the function, the code might raise a SQL exception due to invalid syntax. It can find null pointer dereferences, out of bounds reads and writes, 5xx response codes, ...
This is the property that most fuzzers are checking. Fuzzers like AFL have been very successful at finding security-critical bugs. This property is especially effective against memory-unsafe languages and applications sensitive to DoS.
Of course, if f is expected to raise an exception or an error on some inputs, the test should catch those and return success.
Modeling
In many situations you have an alternate version of an algorithm or process (a “test oracle”) that you can use to check your results. The property tests that a function f under test has the same output has a test oracle g:

This property can be used to check an efficient but complex implementation against a slow but simple implementation. It can also be useful when refactoring code to test the new implementation against the old one.
Inversible operations
If the function f under test has an inverse, a good property to test is that applying the function and its inverse on one input outputs the value you started with.

For instance, this could be used to check that applying a list reversal function twice returns the initial list. Importantly, it can also tests codecs and serializers/deserializers.
Deserializers often parse user input, which could be malicious. They are tricky to write correctly and safely. Testing deserializers against random inputs often finds vulnerabilities on the attack surface!
Hard to compute, easy to verify
Some results are complex to compute, but verifying them is relatively easy. Think about the effort to find the prime factors of a number, compared to the ease of verifying that the factors are correct. In this instance, the test function would look something like the following, where solve is the function under test:
In fact, all the NP problems (and more!) fall in that category. Finding a valid assignment for a SAT formula takes exponential time, but checking that an assignment evaluates to true is polynomial.
Invariants
Invariants are checks or assertions that should be true on all inputs. For instance, an invariant for a filter function could be that filtering does not change the order of elements.
Assertions in the functions under test are also invariants. Adding those extra assertions allow the test to check invariants on intermediary results, which gives us additional confidence in our code.
Some programs and functions are too complex to describe with a single invariant. For those, it's often useful to come up with a set of invariants that should always be true. While no single invariant checks that the output is entirely correct, a combination of multiple invariants gives us increased confidence that the implementation is correct.
Strong ropes are built from smaller threads put together.
- Fred Hebert, author of Property-Based Testing with PropEr, Erlang, and Elixir
Sort is a good example of a function that can be checked with invariants. One important invariant of a sort function is that the output should be sorted. In particular, each number in a sorted list is smaller than (or equal to) the one that follows.
When writing invariants, it's a good exercise to think of alternative implementations that would satisfy the invariants, but that would not be correct. For instance, a "sort" function returning an empty list would satisfy the invariant above, but no one would describe that function as a sort. So what other invariants define a sort function? One answer is that the output should be a permutation of the input. There are multiple ways to check that invariant, even partially:
- The input and output lists should have the same size
- Each element in the input list should appear in the output list, and vice versa.
The list of invariants one may write is endless, and will depend on the function under tests. Mathematical properties of functions can often be used effectively to check functions:
- Associativity:

- Commutativity:

- Commutativity under composition:

- Idempotence:

Conclusion
Property-based Fuzzing combines the power of fuzzing with the properties of property-based testing. It enables us to find more than just crashes and panics. With this technique, we can find correctness bugs even when the program does not crash. We can even find efficiency bugs in some cases.
We encourage you to apply some of those techniques when you write your next fuzzing harness, especially if it’s in a memory-safe language.
Want to know more? Here are a few resources to get you started.
- https://fsharpforfunandprofit.com/posts/property-based-testing-2
- https://blog.johanneslink.net/2018/07/16/patterns-to-find-properties/
- http://citeseerx.ist.psu.edu/viewdoc/download?rep=rep1&type=pdf&doi=10.1.1.216.282
Add Mayhem to Your DevSecOps for Free.
Get a full-featured 30 day free trial.



.jpg)